次の図に示す三角形 \(ABC\) には、次の余弦定理が成り立ちます。
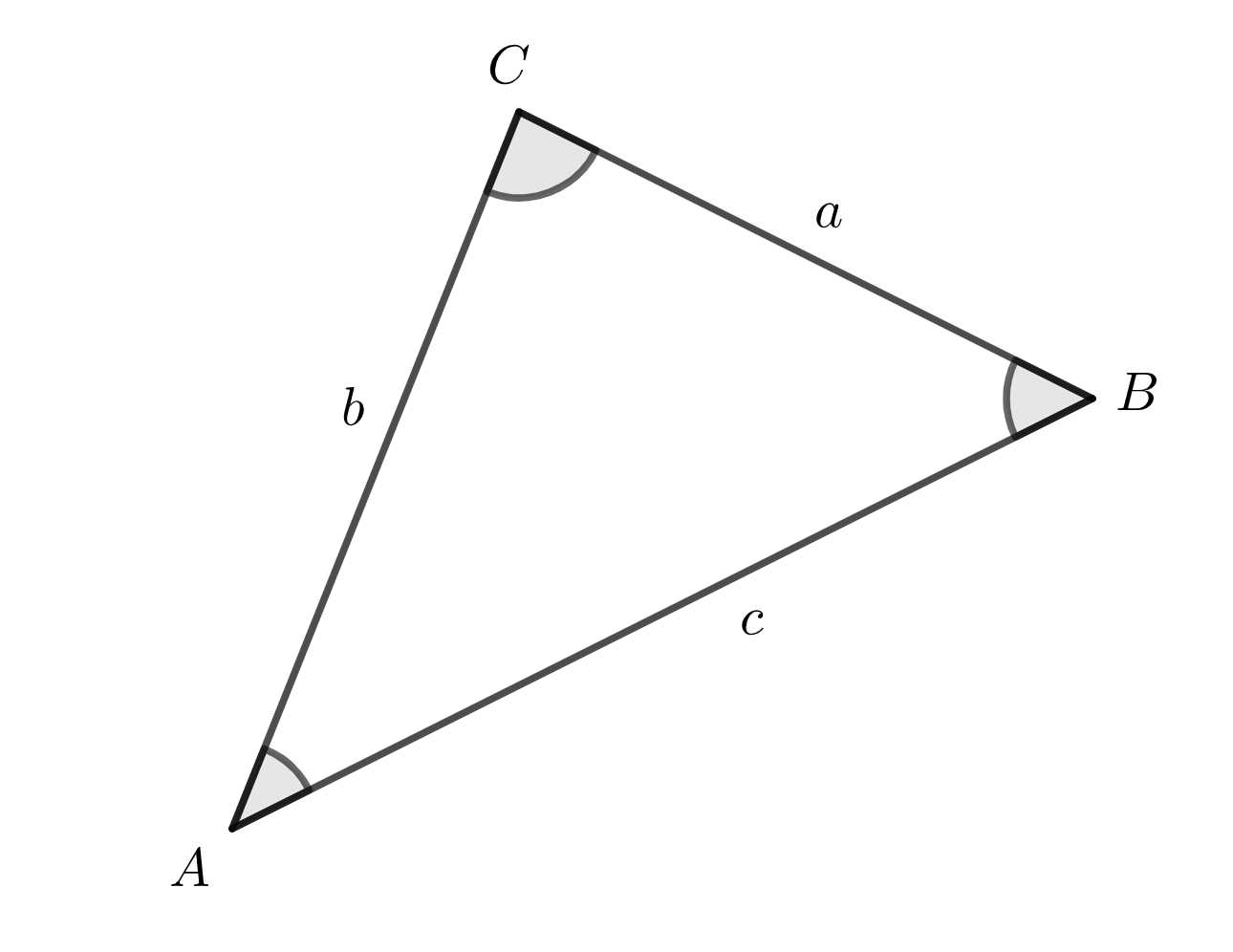
今回は、この余弦定理を証明します。
余弦定理の証明(角 \(A\) が鋭角の場合)
次の図に示すように、頂点 \(C\) から辺 \(AB\) に対して垂線を下ろし、その足を \(H\) とします。
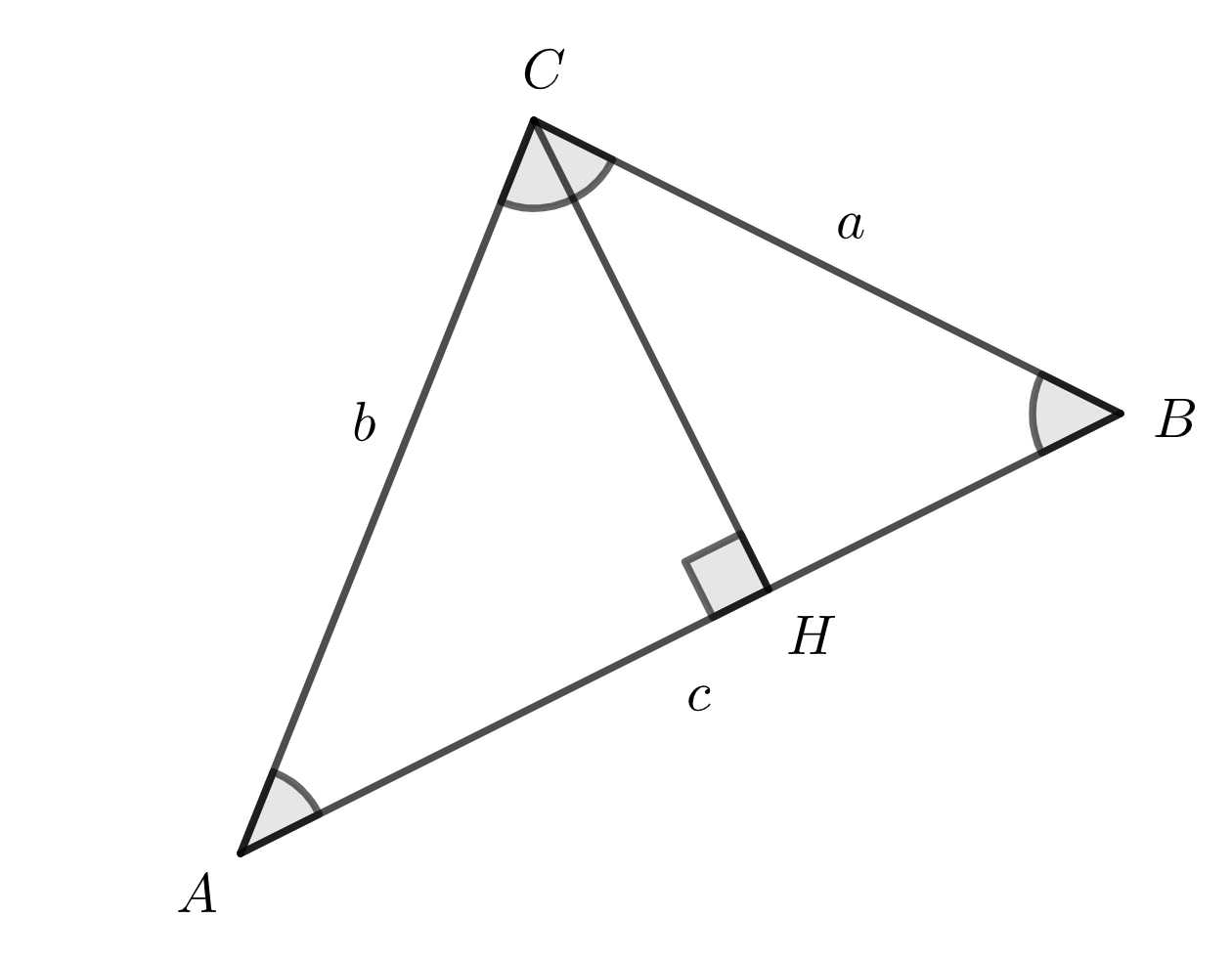
ここで、三角形 \(ACH\) に対して三平方の定理を適応すると、\(b^2=AH^2+CH^2\) となり、次の式が成り立ちます。
\begin{align}
CH^2 = b^2 – AH^2 = b^2 – (b\cos A)^2 \\
\end{align}
CH^2 = b^2 – AH^2 = b^2 – (b\cos A)^2 \\
\end{align}
同様に、三角形 \(BCH\) に対して三平方の定理を適応すると、\(a^2=BH^2+CH^2\) となり、次の式が成り立ちます。
\begin{align}
CH^2 = a^2 – BH^2 = a^2 – (c – AH)^2 = a^2 – (c – b\cos A)^2 \\
\end{align}
CH^2 = a^2 – BH^2 = a^2 – (c – AH)^2 = a^2 – (c – b\cos A)^2 \\
\end{align}
上の二つの式から、次の式が求まります。
\begin{align}
b^2 – (b\cos A)^2 &= a^2 – (c – b\cos A)^2 \\
&= a^2 – (c^2 – 2bc\cos A + b^2 \cos^2 A) \\
\end{align}
b^2 – (b\cos A)^2 &= a^2 – (c – b\cos A)^2 \\
&= a^2 – (c^2 – 2bc\cos A + b^2 \cos^2 A) \\
\end{align}
上の式を整理すると、次のように余弦定理が求められます。
\begin{align}
a^2 &= b^2 – b^2 \cos^2 A + c^2 – 2bc\cos A + b^2 \cos^2 A \\
&= b^2 + c^2 – 2bc\cos A \\
\end{align}
a^2 &= b^2 – b^2 \cos^2 A + c^2 – 2bc\cos A + b^2 \cos^2 A \\
&= b^2 + c^2 – 2bc\cos A \\
\end{align}
余弦定理の証明(角 \(A\) が直角の場合)
角 \(A\) が直角の場合、次の図に示すように、三平方の定理 \(a^2 = b^2 + c^2\) そのものとなります。
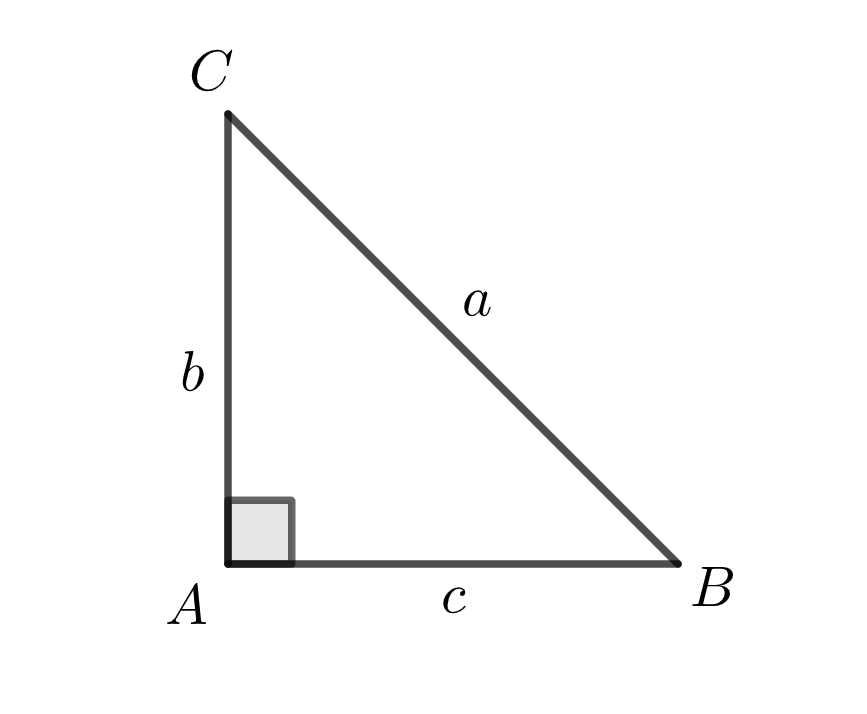
ここで、\(\cos A=\cos \frac{\pi}{2}=0\) となるため、余弦定理が成り立ちます。
\begin{align}
a^2 = b^2 + c^2 – 2bc\cos A \\
\end{align}
a^2 = b^2 + c^2 – 2bc\cos A \\
\end{align}
余弦定理の証明(角 \(A\) が鈍角の場合)
角 \(A\) が鈍角の場合、次の図に示すように、頂点 \(C\) から辺 \(AB\) の延長線上に対して垂線を下ろし、その足を \(H\) とします。

ここで、 \(CH\) と \(AH\) は次のように求められます。
\begin{align}
CH = b\sin (\pi – A) = b\sin A \\
AH = b\cos (\pi – A) = – b\cos A
\end{align}
CH = b\sin (\pi – A) = b\sin A \\
AH = b\cos (\pi – A) = – b\cos A
\end{align}
続いて、三角形 \(BCH\) に対して三平方の定理を適応すると、次のように余弦定理が求められます。
\begin{align}
a^2 &= CH^2 + BH^2 \\
&= (b\sin A)^2 + (c – b\cos A)^2 \\
&= b^2 \sin^2 A + c^2 -2bc \cos A + b^2 \cos^2 A \\
&= b^2(\sin^2 A + \cos^2 A) + c^2 -2bc \cos A \\
&= b^2 + c^2 -2bc \cos A
\end{align}
a^2 &= CH^2 + BH^2 \\
&= (b\sin A)^2 + (c – b\cos A)^2 \\
&= b^2 \sin^2 A + c^2 -2bc \cos A + b^2 \cos^2 A \\
&= b^2(\sin^2 A + \cos^2 A) + c^2 -2bc \cos A \\
&= b^2 + c^2 -2bc \cos A
\end{align}
最後に
今回は、余弦定理 \(a^2 = b^2 + c^2 – 2bc \cos A\) を証明しました。他の2つの式も同様に証明できるので、気になる方はぜひ挑戦してみてください。




コメント