生成AIを理解するには、確率論を理解しておく必要があります。
そこで今回は、確率論の基礎の基礎である「確率変数と確率分布」について説明します。
確率変数と確率分布について
まず、確率変数とは、取り得る値が確率的に決まる変数のことです。たとえば、1から6の目が出るサイコロを振ったときに出る目がそうです。
そこで、サイコロの目を確率変数 \(x\) で表します。そして、ある目が出る確率を \(p(x)\) で表します。たとえば、サイコロの目で1が出る確率は、\(p(x=1)\) と表記します。
続いて、確率分布は、起こり得るすべての値に対して、その確率が示されたものです。サイコロの例では、\(\{1,2,3,4,5,6\}\) の各値に対しての確率を表したものが確率分布になります。
たとえば、次の表がサイコロの確率分布になります。
| サイコロの目 \(x\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| 確率 \(p(x)\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) |
上の表のように、起こり得るすべての値に対して確率が示されるとき、「確率変数 \(x\) は、表の確率分布に従う」と言います。この確率分布をもとに、実際の値が生成されます。
この確率分布から実際に得られたデータひとつひとつの値を観測値 (Observation) や観測データと呼びます。そして、観測値の集合 \(\{2,3,5,\ldots,1\}\) をサンプル (Sample) や標本と呼びます。
なお、上の表のように、各目の出る確率が同じ確率分布を、一様分布 (Uniform Distribution) と呼びます。もちろん、サイコロの確率分布は、一様分布以外にも存在しますが、次の2つの条件を満たす必要があります。
確率分布の種類
確率分布は、離散型確率分布と連続型確率分布の2つに分けられます。
離散型確率分布は、先ほど説明したサイコロの目のように、確率変数が離散(\(1, 2, 3\) のような飛び飛びの値)で、連続型確率分布は、身長や気温などのように、確率変数が連続値を取ります。
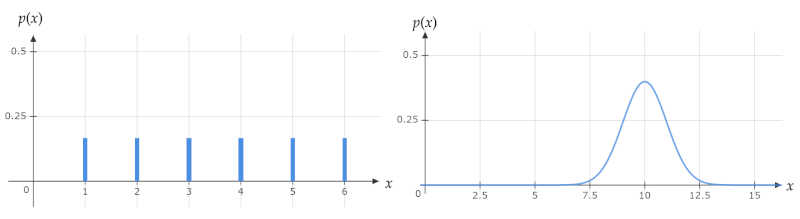
上図(左)に示すように、離散型確率変数の場合、\(p(x)\) は確率を表します。一方、上図(右)に示すように、連続型確率変数の場合、\(p(x)\) は確率密度を表します。確率密度 \(p(x)\) は、確率密度関数とも呼ばれます。
そのため、連続型確率分布の場合は、確率密度 \(p(x)\) をそのまま確率として扱えません。
そこで、\(x\) が特定の区間にある確率を、特定の区間の曲線下の面積で求めます。たとえば、身長が170cm以上、180cm以下の確率は、\(\int_{170}^{180} p(x) dx\) として求めることができます。
連続型確率分布も、確率分布として成立するために、次の2つの条件を満たす必要があります。
最後に
今回は、確率論の基礎の基礎である「確率変数と確率分布」について説明しました。確率分布を扱うときは、連続型か離散型か意識しましょう。




コメント