【高校数学】三角関数の相互関係とは

　三角関数の相互関係とは、\(\sin \theta, \cos \theta, \tan \theta\) の間に成り立つ関係のことです。今回は、三角関数の相互関係の紹介とその証明を行います。

三角関数の相互関係の定義
三角関数の相互関係の証明
最後に

三角関数の相互関係の定義

　三角関数の相互関係は、次のように定義されます。

\begin{align}
& \sin^2 \theta + \cos^2 \theta = 1 \\
& \tan \theta = \frac{\sin \theta}{\cos \theta} \\
& 1 + \tan^2 \theta = \frac{1}{\cos^2 \theta} \\
\end{align}

三角関数の相互関係の証明

　では、三角関数の相互関係を証明していきます。

　まず、次の図に示すような単位円を考えます。

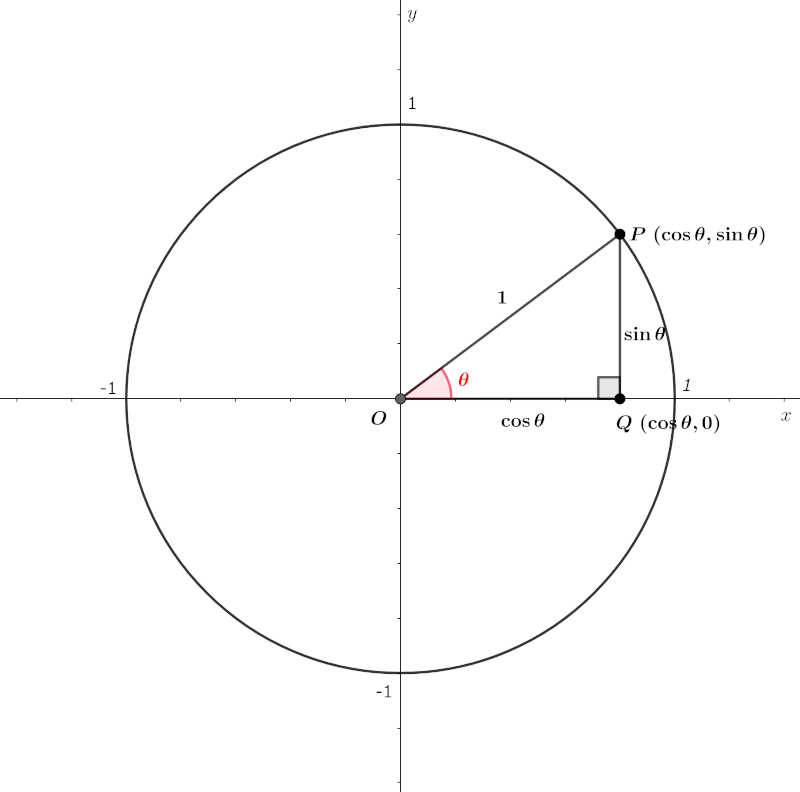
　ここで、三角関数の定義を思い出しましょう。三角関数は、次のように定義されました。

\begin{align}
& \sin \theta = \frac{PQ}{OP} = PQ \\
& \cos \theta = \frac{OQ}{OP} = OQ \\
& \tan \theta = \frac{PQ}{OQ}
\end{align}

　上の式では、単位円のため、\(OP = 1\) になることを用いています。

\(\sin^2 \theta + \cos^2 \theta = 1\) の証明

　三角形 \(OPQ\) に対して、三平方の定理を用いると、三角関数の相互関係の1つ目の式が求められます。

\begin{align}
& PQ^2 + OQ^2 = OP^2 \\
& \Leftrightarrow \sin^2 \theta + \cos^2 \theta = 1 \\
\end{align}

\(\tan \theta = \frac{\sin \theta}{\cos \theta}\) の証明

　\(\sin \theta = PQ, \cos \theta = OQ\) を \(\tan \theta\) の式に代入すると、三角関数の相互関係の2つ目の式が求められます。

\begin{align}
& \tan \theta = \frac{PQ}{OQ} = \frac{\sin \theta}{\cos \theta}
\end{align}

\(1 + \tan^2 \theta = \frac{1}{\cos^2 \theta}\) の証明

　ここまで証明した三角関数の相互関係を使うと、三角関数の相互関係の3つ目の式が求められます。

\begin{align}
1 + \tan^2 \theta &= 1 + \frac{\sin^2 \theta}{\cos^2 \theta} \\
&= \frac{\sin^2 \theta + \cos^2 \theta}{\cos^2 \theta} \\
&= \frac{1}{\cos^2 \theta}
\end{align}