内積とは／内積の成分表示とは

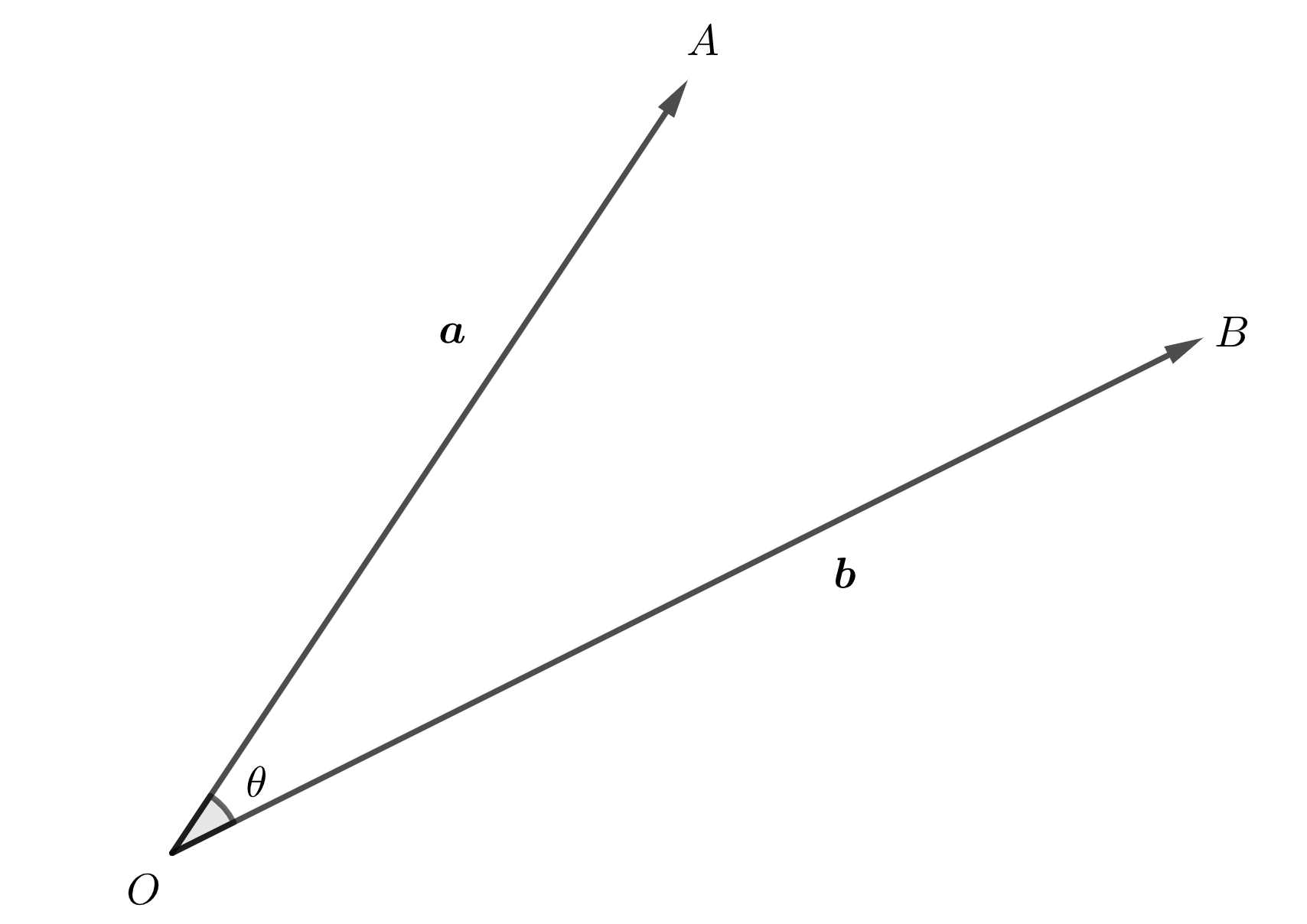
　ベクトル \(\boldsymbol{a}, \boldsymbol{b}\) のなす角を \(\theta\) とすると、内積 \(\boldsymbol{a} \cdot \boldsymbol{b}\) は、次の式で表されます。

■内積
\begin{align}
\boldsymbol{a} \cdot \boldsymbol{b} = |\boldsymbol{a}||\boldsymbol{b}| \cos {\theta}
\end{align}
■内積の成分表示（2次元の場合）
\begin{align}
\boldsymbol{a} \cdot \boldsymbol{b} = a_x b_x + a_y b_y
\end{align}

　今回は、内積の意味と内積の成分表示について説明します。

内積とは
内積の成分表示とは
最後に

内積とは

　物体に大きさ \(f\) の力が働き、物体が力と同じ方向に \(l\) だけ移動した場合、物体がした仕事は \(f \times l\) となります。

　しかし、物体は必ずしも加えられた力の方向に動くとは限りません。そこで、物体に力 \(\boldsymbol{f}\) を加えたとき、次の図のように点 \(A\) から点 \(B\) まで移動したとします。

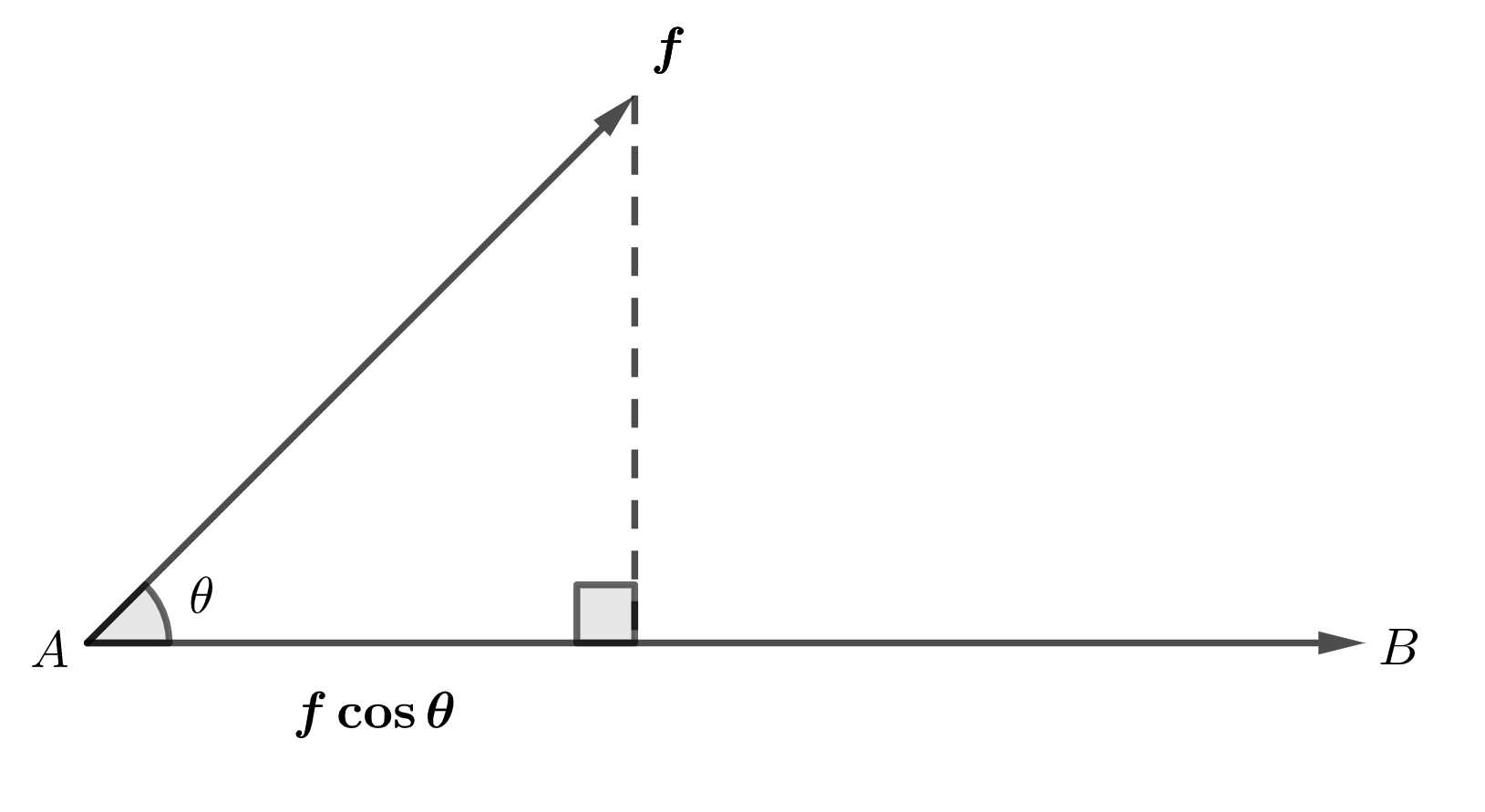
　このとき、この物体がした仕事は、力の移動方向への正射影×移動距離となるため、次の式で求められます。

\begin{align}
|\boldsymbol{f}| \cos {\theta} \times |\boldsymbol{AB}| = |\boldsymbol{f}||\boldsymbol{AB}|\cos {\theta} \\
\end{align}

　このベクトル同士の積を内積といい、一般的には次の図に示すような2つのベクトル \(\boldsymbol{a}, \boldsymbol{b}\) のなす角を \(\theta\) とすると、\(\boldsymbol{a} \cdot \boldsymbol{b} = |\boldsymbol{a}||\boldsymbol{b}| \cos {\theta}\) で表すことができます。

内積の成分表示とは

　次の図に示す2つのベクトル \(\boldsymbol{a}, \boldsymbol{b}\) の成分表示を \(\boldsymbol{a}=(a_x, a_y), \boldsymbol{b}=(b_x, b_y)\) とします。

　ここで、三角形 \(OAB\) に対して余弦定理を適用すると、次のようになります。

\begin{align}
AB^2 &= OA^2 + OB^2 – 2OA \times OB \times \cos {\theta} \\
|\boldsymbol{b-a}|^2 &= |\boldsymbol{a}|^2 + |\boldsymbol{b}|^2 – 2|\boldsymbol{a}||\boldsymbol{b}|\cos {\theta} \\
\end{align}

　ここで、上の式に対して成分表示 \(\boldsymbol{a}=(a_x, a_y), \boldsymbol{b}=(b_x, b_y)\) をすると次のようになります。

\begin{align}
(b_x – a_x)^2 + (b_y – a_y)^2 &= a_x^2 + a_y^2 + b_x^2 + b_y^2 -2 |\boldsymbol{a}||\boldsymbol{b}|\cos {\theta} \\
-2 a_x b_x -2 a_y b_y &= -2 |\boldsymbol{a}||\boldsymbol{b}|\cos {\theta} \\
a_x b_x + a_y b_y &= |\boldsymbol{a}||\boldsymbol{b}|\cos {\theta} \\
\end{align}

　ここで、内積の定義 \(\boldsymbol{a} \cdot \boldsymbol{b} = |\boldsymbol{a}||\boldsymbol{b}| \cos {\theta}\) より、次のように内積の成分表示を求めることができます。

\begin{align}
\boldsymbol{a} \cdot \boldsymbol{b} = a_x b_x + a_y b_y \\
\end{align}