【高校数学】三角関数の合成公式とは

　三角関数の合成公式とは、三角関数の「\(\sin\) と \(\cos\) の和」を「\(\sin\) または \(\cos\)」にまとめる公式のことです。今回は、三角関数の合成公式の紹介とその証明を行います。

三角関数の合成公式の定義
三角関数の積和公式の証明
1. \(a \sin \theta + b \cos \theta = \sqrt{a^2+b^2} \sin (\theta + \alpha)\) の証明
2. \(a \sin \theta + b \cos \theta = \sqrt{a^2+b^2} \cos (\theta – \beta)\) の証明
最後に

三角関数の合成公式の定義

　三角関数の合成公式は、次のように定義されます。

\begin{align}
& a \sin \theta + b \cos \theta = \sqrt{a^2+b^2} \sin (\theta + \alpha) \\
& a \sin \theta + b \cos \theta = \sqrt{a^2+b^2} \cos (\theta – \beta) \\
\end{align}

　ただし、\(\alpha, \beta\) は、次の式を満たす必要があります。

\begin{align}
& \sin \alpha = \frac{b}{\sqrt{a^2+b^2}},\ \cos \alpha = \frac{a}{\sqrt{a^2+b^2}} \\
& \sin \beta = \frac{a}{\sqrt{a^2+b^2}},\ \cos \beta = \frac{b}{\sqrt{a^2+b^2}} \\
\end{align}

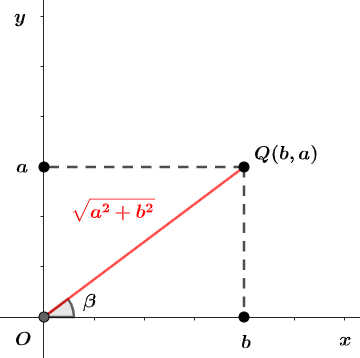
　それぞれ図で表すと、次のようになります。

三角関数の積和公式の証明

　では、三角関数の合成公式を証明していきます。

\(a \sin \theta + b \cos \theta = \sqrt{a^2+b^2} \sin (\theta + \alpha)\) の証明

　次に示す \(\sin\) の加法定理を用います。

\begin{align}
\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\
\end{align}

　\(\sin\) の加法定理より、合成公式の右辺は次のように展開できます。

\begin{align}
\sqrt{a^2+b^2} \sin (\theta + \alpha) = \sqrt{a^2+b^2} (\sin \theta \cos \alpha + \cos \theta \sin \alpha) \\
\end{align}

　ここで、\(\alpha\) は次の図に示す角度のため、\(\sin \alpha = \frac{b}{\sqrt{a^2+b^2}}, \ \cos \alpha = \frac{a}{\sqrt{a^2+b^2}}\) となります。

　これらを元の式に代入すると、\(\sin\) の三角関数の合成公式が次のように求められます。

\begin{align}
\sqrt{a^2+b^2} \sin (\theta + \alpha) &= \sqrt{a^2+b^2} (\sin \theta \cos \alpha + \cos \theta \sin \alpha) \\
&= \sqrt{a^2+b^2} \left(\frac{a \sin \theta}{\sqrt{a^2+b^2}} + \frac{b \cos \theta}{\sqrt{a^2+b^2}}\right) \\
&= a \sin \theta + b \cos \theta \\
\end{align}

\(a \sin \theta + b \cos \theta = \sqrt{a^2+b^2} \cos (\theta – \beta)\) の証明

　次に示す \(\cos\) の加法定理を用います。

\begin{align}
\cos (\alpha – \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \\
\end{align}

　\(\cos\) の加法定理より、合成公式の右辺は次のように展開できます。

\begin{align}
\sqrt{a^2+b^2} \cos (\theta – \beta) = \sqrt{a^2+b^2} (\cos \theta \cos \beta + \sin \theta \sin \beta) \\
\end{align}

　ここで、\(\beta\) は次の図に示す角度のため、\(\sin \beta = \frac{a}{\sqrt{a^2+b^2}}, \ \cos \beta = \frac{b}{\sqrt{a^2+b^2}}\) となります。

　これらを元の式に代入すると、\(\cos\) の三角関数の合成公式が次のように求められます。

\begin{align}
\sqrt{a^2+b^2} \cos (\theta – \beta) &= \sqrt{a^2+b^2} (\cos \theta \cos \beta + \sin \theta \sin \beta) \\
&= \sqrt{a^2+b^2} \left(\frac{b \cos \theta}{\sqrt{a^2+b^2}} + \frac{a \sin \theta}{\sqrt{a^2+b^2}}\right) \\
&= b \cos \theta + a \sin \theta \\
\end{align}