三角関数の余角・補角・負角の公式とは、\(\sin \left(\frac{\pi}{2}-\theta \right), \sin (\pi-\theta), \sin (-\theta)\) を求める公式のことです。今回は、三角関数の余角・補角・負角の公式の紹介とその証明を行います。
三角関数の余角・補角・負角の公式
三角関数の余角・補角・負角の公式は、次のように定義されます。
三角関数の余角・補角・負角の公式の証明
では、三角関数の余角・補角・負角の公式を証明していきます。
三角関数の余角の公式の証明
次の図に示すような単位円を考えます。
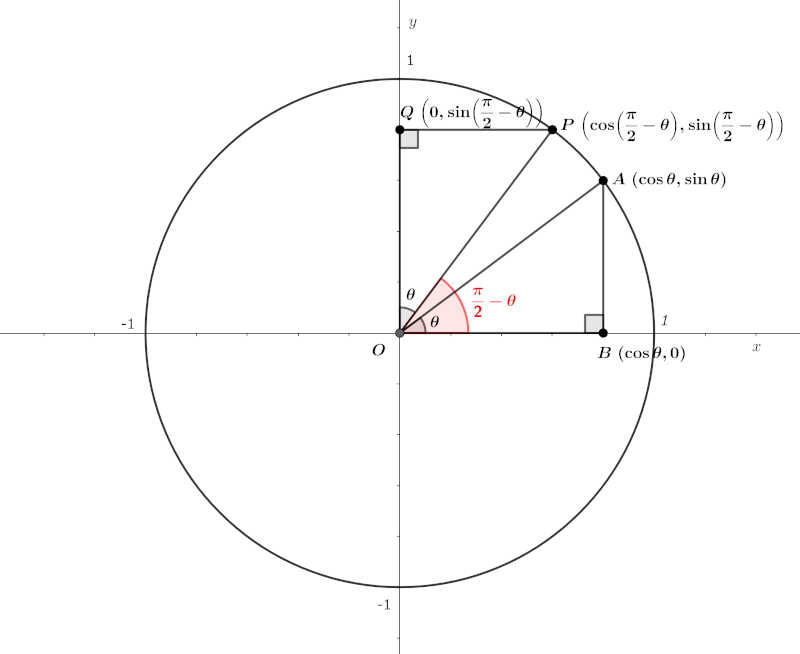
ここで、三角形 \(OAB\) と三角形 \(OPQ\) は等しいため、\(AB=PQ, OB=OQ\) となり、\(\sin \left(\frac{\pi}{2}-\theta \right), \cos \left(\frac{\pi}{2}-\theta \right)\) が求められます。
& AB = \sin \theta = \cos \left(\frac{\pi}{2}-\theta \right) = PQ \\
& OB = \cos \theta = \sin \left(\frac{\pi}{2}-\theta \right) = OQ \\
\end{align}
また、上の式を用いて、\(\tan \left(\frac{\pi}{2}-\theta \right)\) が次のように求められます。
\tan \left(\frac{\pi}{2}-\theta \right) &= \frac{\sin \left(\frac{\pi}{2}-\theta \right)}{\cos \left(\frac{\pi}{2}-\theta \right)} \\
&= \frac{\cos \theta}{\sin \theta} \\
&= \frac{1}{\tan \theta} \\
\end{align}
三角関数の補角の公式の証明
次の図に示すような単位円を考えます。
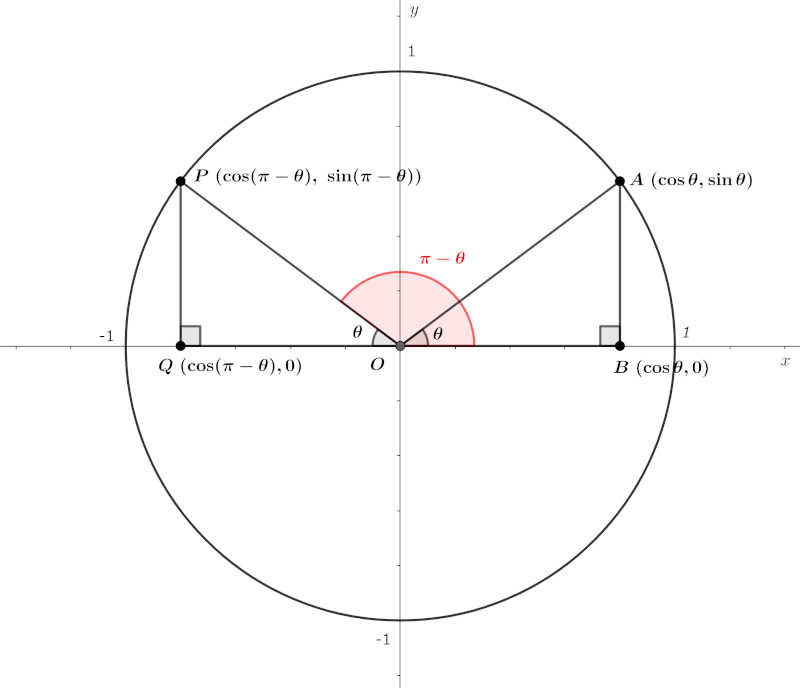
ここで、三角形 \(OAB\) と三角形 \(OPQ\) は等しいため、\(AB=PQ, OB=-OQ\) となり、\(\sin (\pi-\theta), \cos (\pi-\theta)\) が求められます。
補足:\(OB=-OQ\) となるのは、点 \(Q\) の \(x\) 座標がマイナスの領域にあるからです。
& AB = \sin \theta = \sin (\pi-\theta) = PQ \\
& OB = \cos \theta = – \cos (\pi-\theta) = -OQ \\
\end{align}
また、上の式を用いて、\(\tan (\pi-\theta)\) が次のように求められます。
\tan (\pi-\theta) &= \frac{\sin (\pi-\theta)}{\cos (\pi-\theta)} \\
&= \frac{\sin \theta}{-\cos \theta} \\
&= -\tan \theta \\
\end{align}
三角関数の負角の公式の証明
次の図に示すような単位円を考えます。
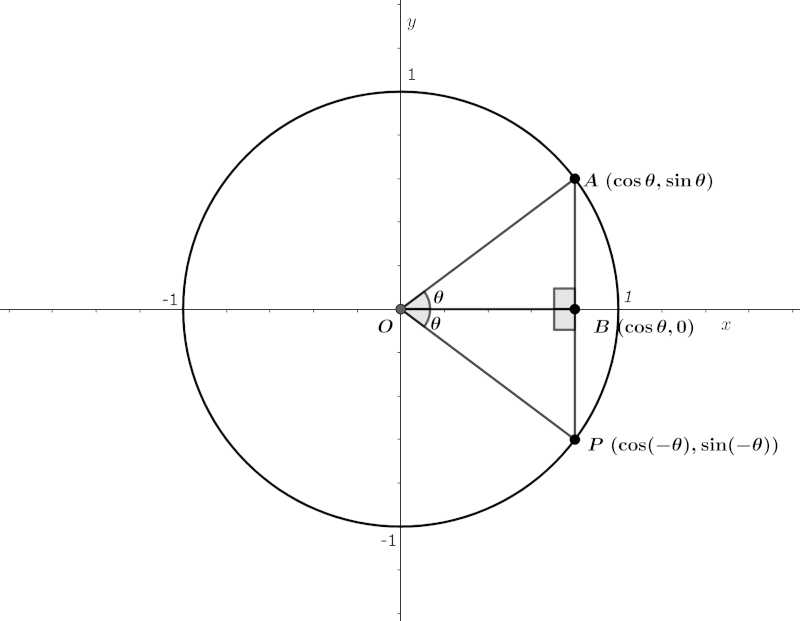
ここで、三角形 \(OAB\) と三角形 \(OPB\) は等しいため、\(AB=-PB, OB=OB\) となり、\(\sin (-\theta), \cos (-\theta)\) が求められます。
補足:\(AB=-PB\) となるのは、点 \(P\) の \(y\) 座標がマイナスの領域にあるからです。
& AB = \sin \theta = -\sin (-\theta) = -PB \\
& OB = \cos \theta = \cos (-\theta) = OB \\
\end{align}
また、上の式を用いて、\(\tan (-\theta)\) が次のように求められます。
\tan (-\theta) &= \frac{\sin (-\theta)}{\cos (-\theta)} \\
&= \frac{-\sin \theta}{\cos \theta} \\
&= -\tan \theta \\
\end{align}
最後に
今回は、「三角関数の余角・補角・負角の公式」について説明しました。いつでも導出できるように、図をイメージできるようにしておきましょう。




コメント