三角関数の加法定理とは、三角関数における2つの角度 \(\alpha, \beta\) の足し算を求める式のことです。今回は、三角関数の加法定理の紹介とその証明を行います。
三角関数の加法定理の定義
三角関数の加法定理は、次のように定義されます。
三角関数の加法定理の証明
では、三角関数の加法定理を証明していきます。
\(\cos (\alpha + \beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta\) の証明
次の図に示すように、単位円上の点 \(Q \ (\cos (\alpha + \beta), \sin (\alpha + \beta))\) を考えます。あわせて、\(A, P, R\) を用意します。
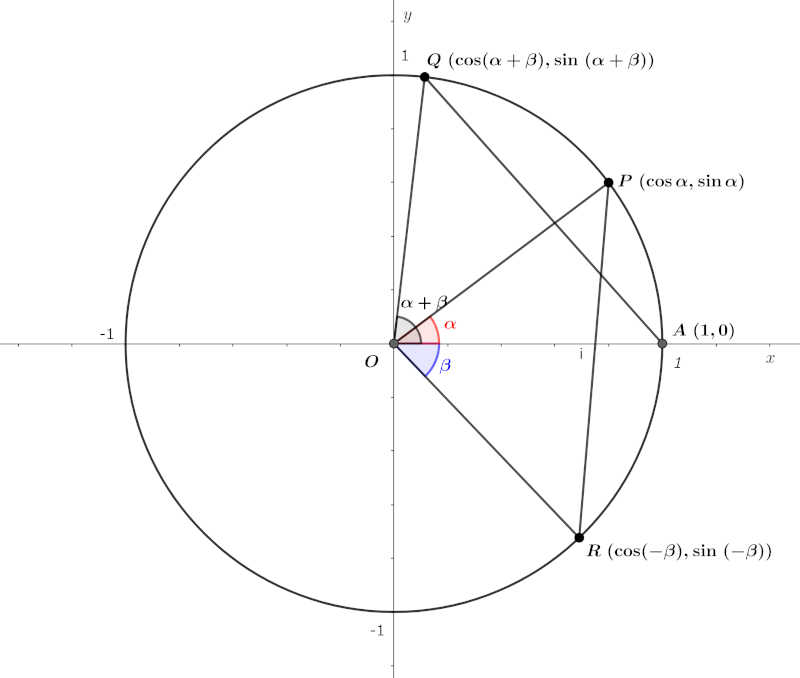
ここで上の図より、\(RP\) を原点周りに \(\beta\) だけ回転すると、\(AQ\) になることが明らかなため、\(RP=AQ\) となります。
そこで、2点間の距離の公式を用いると、次の式が成り立ちます。
AQ&=\sqrt{(\cos(\alpha+\beta)-1)^2+(\sin(\alpha+\beta)-0)^2} \\
&= \sqrt{(\cos (-\beta) – \cos \alpha)^2+(\sin(-\beta)-\sin \alpha)^2} = RP
\end{align}
続いて、負角の公式 \(\cos (-\beta)=\cos \beta,\ \sin(-\beta)=-\sin \beta\) を代入すると、次のようになります。
\sqrt{(\cos(\alpha+\beta)-1)^2+\sin^2(\alpha+\beta)} = \sqrt{(\cos \beta – \cos \alpha)^2+(-\sin\beta-\sin \alpha)^2}
\end{align}
上の式の両辺を2乗してから展開すると、次のようになります。
&\cos^2(\alpha+\beta)-2\cos(\alpha+\beta)+1^2+\sin^2(\alpha+\beta) \\
&= \cos^2 \beta -2 \cos \beta \cos \alpha + \cos^2 \alpha + \sin^2\beta + 2 \sin \beta \sin \alpha + \sin^2 \alpha
\end{align}
さらに、三角関数の相互関係 \(\cos^2 \theta + \sin^2 \theta=1\) を用いて、上の式を整理すると、次のように \(\cos\) の加法定理が求まります。
&-2\cos(\alpha+\beta)+2 = 2 -2 \cos \beta \cos \alpha + 2 \sin \beta \sin \alpha \\
& \Leftrightarrow -2\cos(\alpha+\beta) = -2 \cos \beta \cos \alpha + 2 \sin \beta \sin \alpha \\
& \Leftrightarrow \cos(\alpha+\beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta \\
\end{align}
ちなみに、\(\cos (\alpha + \beta)\) の \(\beta\) を \(-\beta\) に置き換えると、次の式が求まります。
& \cos (\alpha – \beta) = \cos \alpha \cos (-\beta) – \sin \alpha \sin (-\beta) \\
& \Leftrightarrow \cos (\alpha – \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \\
\end{align}
上の式展開では、負角の公式 \(\cos (-\beta)=\cos \beta,\ \sin(-\beta)=-\sin \beta\) を用いています。
\(\sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta\) の証明
まず、\(\sin (\alpha + \beta)\) に、余角の公式 \(\cos \left(\frac{\pi}{2}-\theta \right) = \sin \theta\) を用います。
\sin (\alpha + \beta) &= \cos \left(\frac{\pi}{2}-(\alpha + \beta) \right) \\
&= \cos \left(\left(\frac{\pi}{2} – \alpha \right)+(-\beta) \right) \\
\end{align}
続いて、先ほど求めた \(\cos\) の加法定理 \(\cos (\alpha + \beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta\) を用います。
\sin (\alpha + \beta) &= \cos \left(\left(\frac{\pi}{2} – \alpha \right)+(-\beta) \right) \\
&= \cos \left(\frac{\pi}{2} – \alpha \right)\cos (-\beta) – \sin \left(\frac{\pi}{2} – \alpha \right)\sin (-\beta) \\
\end{align}
さらに、余角の公式 \(\sin \left(\frac{\pi}{2}-\theta \right) = \cos \theta,\ \cos \left(\frac{\pi}{2}-\theta \right) = \sin \theta\) と負角の公式 \(\sin (-\theta) = -\sin \theta, \ \cos (-\theta) = \cos \theta\) を用いて整理すると、次のように \(\sin\) の加法定理が求まります。
\sin (\alpha + \beta) &= \cos \left(\frac{\pi}{2} – \alpha \right)\cos (-\beta) – \sin \left(\frac{\pi}{2} – \alpha \right)\sin (-\beta) \\
&= \sin \alpha \cos \beta – \cos \alpha (-\sin \beta) \\
&= \sin \alpha \cos \beta + \cos \alpha \sin \beta \\
\end{align}
ちなみに、\(\sin (\alpha + \beta)\) の \(\beta\) を \(-\beta\) に置き換えると、次の式が求まります。
& \sin (\alpha – \beta) = \sin \alpha \cos (-\beta) + \cos \alpha \sin (-\beta) \\
& \Leftrightarrow \sin (\alpha – \beta) = \sin \alpha \cos \beta – \cos \alpha \sin \beta \\
\end{align}
上の式展開では、負角の公式 \(\cos (-\beta)=\cos \beta,\ \sin(-\beta)=-\sin \beta\) を用いています。
\(\tan (\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 – \tan \alpha \tan \beta}\) の証明
\(\tan (\alpha + \beta)\) は、ここまで求めた \(\sin (\alpha + \beta), \cos (\alpha + \beta)\) を用いて、次のように求められます。
\tan (\alpha + \beta) &= \frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)} \\
&= \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta – \sin \alpha \sin \beta} \\
&= \frac{\tan \alpha + \tan \beta}{1 – \tan \alpha \tan \beta} \\
\end{align}
最後の行は、分母分子を \(\cos \alpha \cos \beta\) で割っています。
\(\tan (\alpha – \beta)\) も、\(\sin (\alpha – \beta), \cos (\alpha – \beta)\) を用いて、次のように求められます。
\tan (\alpha – \beta) &= \frac{\sin (\alpha – \beta)}{\cos (\alpha – \beta)} \\
&= \frac{\sin \alpha \cos \beta – \cos \alpha \sin \beta}{\cos \alpha \cos \beta + \sin \alpha \sin \beta} \\
&= \frac{\tan \alpha – \tan \beta}{1 + \tan \alpha \tan \beta} \\
\end{align}
こちらも、最後の行は、分母分子を \(\cos \alpha \cos \beta\) で割っています。
最後に
今回は、「三角関数の加法定理」について説明しました。少し複雑ですが、繰り返し計算して体になじませましょう。






コメント